The QuantOm has collaboration developed an ultra-fast software package called tiktaalik to perform renormalization group evolution of generalized parton distributions. The code uses finite element methods to make the evolution auto-differentiable, allowing it to be used in AI/ML frameworks, such as those being developed by QuantOm.
Background
Evolution equations underpin the global analysis of quantum correlation functions in general—including the generalized parton distributions (GPDs) focused on in this work. These equations essentially describe how the apparent internal structure of hadrons (such as the proton)—characterized as spatial distributions of quarks and gluons—depend on the resolution at which you probe the hadron. In effect, the finer your resolution, the more quarks and gluons you see—and the less of the proton’s momentum they each carry.
Global analysis involves the extraction of GPDs from empirical data at a variety of experimental facilities, including Jefferson Lab and the future Electron Ion Collider. These experiments are performed at disparate energy scales and accordingly probe the proton at exceedingly different resolutions. Evolution of the apparent structure of the proton is thus vital to global analysis.
The Science
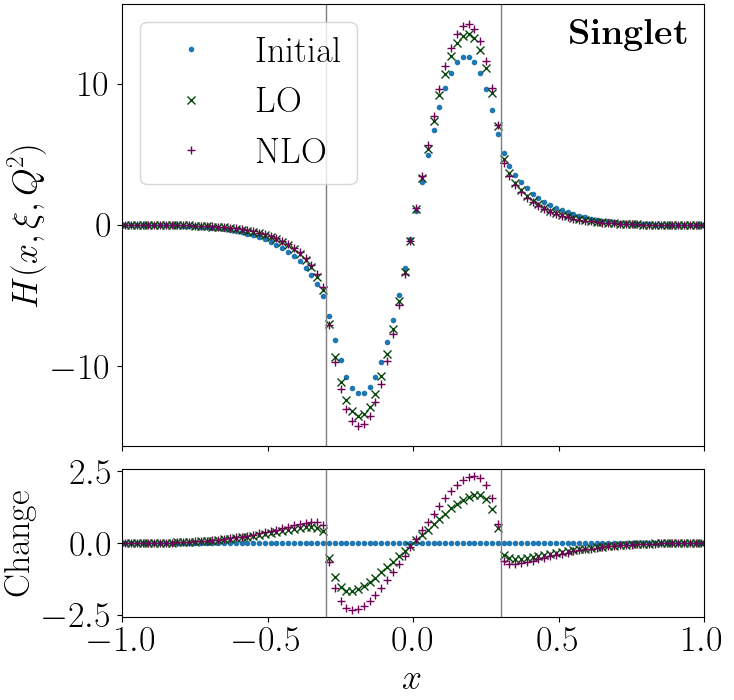
Evolution equations for GPDs are a complicated set of coupled equations that are exceedingly difficult to solve analytically. They are typically solved using approximate computational methods.
Our software package, tiktaalik, uses a modern finite element method to solve the equations. In effect, tiktaalik digitizes the GPD, representing what is in reality a smooth function by a series of discrete pixels—similar to how a phone camera represents a continuous visual reality using a 2D array of pixels. However, a peculiar kind of pixels—pixels that are smooth and overlap slightly—are used, giving them nice mathematical properties that make them easier to evolve. We call these peculiar pixels interpixels—short for interpolated pixels.
tiktaalik computes a matrix that evolves interpixels into other interpixels. This matrix is independent of the particular GPD—independent of the particular image that is being digitized—so it only needs to be computed and initialized once, and stored in memory. Since the digitized GPD is just a series of interpixels, any GPD can be evolved by this matrix through simple matrix multiplication. Matrix multiplication is fast and differentiable, making finite element codes such as tiktaalik ideal for use in modern, AI/ML-based global analysis frameworks.
Contact
Adam Freese (afreese@jlab.org)
Reference
Computer Physics Communications 311 (2025) 109552
GitHub repo
tiktaalik: Fast x-space evolution code for generalized parton distributions based on finite element methods